Solving first degree equations in two unknowns
Any system in the following form is commonly referred to as a system of two linear equations in two unknowns:
ax + by = p
cx + dy = q
Solving by the elimination method.
To solve a system of two linear equations in two unknowns, you must first eliminate one of the unknowns by way of performing operations on the equations.
This technique allows one to obtain a single equation in one unknown, which can then be solved using the methods presented in lesson 11.
Example 1
Solve
E1 2x + y = 4
E2 x - 2y = -3
Performing 2E1 + E2 n order to eliminate the unknown y, we see:
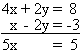
x = 1
In replacing x by 1 in E1 or E2, we obtain y = 2
Solving by the substitution method
To solve a system of two linear equations in two unknowns by the substitution method, it suffices to isolate one of the unknowns in one of the equations, and then to replace this unknown in the other equation with its value.
We thus obtain a single equation in one unknown, which can then be solved according to the method presented in lesson 11.
Example 2
Solve
E1 2x + y = 4
E2 x - 2y = -3
In isolating y in E1, we have: y = 4 - 2x
Upon substituting in E2 the unknown y by its value, we obtain:
x - 2(4-2x) = -3
x - 8 + 4x = -3
5x = 5, x = 1
In replacing x by 1 in E1 or E2, we obtain: y = 2
Before proceeding to the questions, ensure that you have some paper and
a pencil handy.
|| Equations in two unknowns || Next
||