|| Quadratic equations || Next ||

Quadratic equations in one unknown

A second degree equation in one unknown, or a quadratic equation, is any equation in the following form;

ax² + bx + c = 0

where a, b and c are real coefficients.

The general solution to such an equation is given by the following formula, called the quadratic formula;

If b² -4ac > 0, then the equation has two distinct roots.
If b² -4ac = 0, then the equation has a double root.
If b² -4ac < 0, then the equation has no real solutions.

Example 1

Solve 2x² - 2x - 4 = 0

In this example,, a=2, b= -2 and c= -4

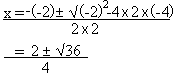
x₁ = 2 and x₂ = -1

This equation has two distinct roots.

Example 2

Solve x² - 6x + 9 = 0

Here a = 1, b = -6 and c = 9

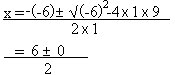
x₁ = 3 and x₂ = 3

This equation is said to have a double root.

Example 3

Solve x² + x + 7 = 0

In this example, a=1, b = 1, and c = 7

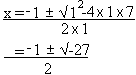
However, the square root of a negative number is not defined in the real numbers. Thus, the equation has no solution.

Before proceeding to the questions, ensure that you have some paper and a pencil handy.


|| Quadratic equations || Next ||