Trigonometry of a right triangle
Given a right triangle ABC, we define the following trigonometric relations:
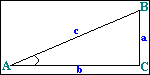sin A = a/c
cosec A = 1/sin
A = c/a
cos A = b/c
sec A = 1/cos
A = c/b
tan A = a/b
cotan A = 1/tan A = b/a
Example 1
Consider the right triangle ABC, for which the length of the sides is provided in the adjacent diagram.
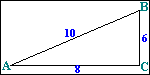Then
sin A=6/10= 0.6000
cosec A=10/6
= 1.6666
cos A=8/10= 0.8000
sec A=10/8
= 1.2500
tan A=6/8 = 0.7500
cotan A=8/6
= 1.3333
Example 2
With the help of a calculator, evaluate:
a) sin 37°
b) cos 72°
c) tan 128°
d) sec 43°
e) cosec 122°
Answers
a) sin 37° = 0.6018
b) cos 72° = 0.3090
c) tan 128° = -1.2799
d) sec 43° = 1/cos 43° = 1.3673
e) cosec 122° = 1/sin 122° = 1.1792
Example 3
Find the length of the sides a and b of the right triangle in the diagram.
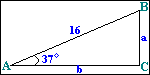Solution
Since sin 37° = a/16
therefore a = 16 X sin37°
and a = 16 X (0.6018)
a = 9.63
Because cos 37° = b/16
therefore b = 16 X cos37°
and b = 16 X (0.7986)
b = 12.78
N. B. We can also find the length of the side b by applying the Pythagorean theorem.
In effect, b = 
162
b = 162
- (9.63)2
b = 12.78
Before proceeding to the questions, ensure that you have a pencil, some
paper, and a calculator handy.
|| Trigonometry || Next
||