Équations quadratiques à une inconnue
On appelle équation du second degré, à une inconnue ou équation quadratique, toute équation de la forme
ax2 + bx + c = 0
où a, b et c sont des coefficients réels.
La solution générale de l'équation est donnée par la formule
![]()
Si b2 -4ac > 0, alors l'équation a deux racines distinctes.
Si b2 -4ac = 0, alors l'équation a une racine double.
Si b2 -4ac < 0, alors l'équation n'a pas de solution.
Exemple 1
Résoudre 2x2 - 2x - 4 = 0
Dans cet exemple, a=2, b= -2 et c= -4
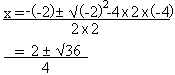
x1 = 2 et x2 = -1
L'équation a deux racines distinctes.
Exemple 2
Résoudre x2 - 6x + 9 = 0
Ici a = 1, b = -6 et c = 9
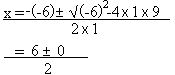
x1 = 3 et x2 = 3
On dit que l'équation a une racine double.
Exemple 3
Résoudre x2 + x + 7 = 0
Dans cet exemple, a=1, b = 1, et c = 7
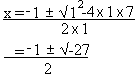
Or, la racine d'un nombre négatif n'est pas définie dans les nombres réels. Donc l'équation n'a pas de solution.
Avant de passer aux questions, assurez-vous d'avoir en votre possession un crayon et du papier.
|| Équations quadratiques || Suite![]() ||
||