Résolution d'équations du premier degré à deux inconnues
On appelle système de deux équations linéaires à deux inconnues, tout système de la forme :
ax + by = p
cx + dy = q
Résolution par la méthode d'élimination.
Pour résoudre un système de deux équations linéaires à deux inconnues, il faut éliminer l'une des inconnues au moyen d'opérations sur les équations.
Cette technique permet d'obtenir une seule équation à une inconnue, que l'on peut résoudre selon la méthode présentée à la leçon 11.
Exemple 1
Résoudre
E1 2x + y = 4
E2 x - 2y = -3
En effectuant 2E1 + E2 pour éliminer l'inconnue y, on obtient :
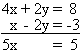
x = 1
En remplaçant x par 1 dans E1 ou E2, on obtient y = 2
Résolution par la méthode de substitution
Pour résoudre un système de deux équations linéaires à deux inconnues par la méthode de substitution, il suffit d'isoler l'une des inconnues dans l'une des équations et de remplacer cette inconnue par sa valeur dans l'autre équation.
On obtient ainsi une équation à une seule inconnue, que l'on peut résoudre selon la méthode présentée à la leçon 11.
Exemple 2
Résoudre
E1 2x + y = 4
E2 x - 2y = -3
En isolant y dans E1, on a: y = 4 - 2x
En substituant dans E2 y par sa valeur, on obtient :
x - 2(4-2x) = -3
x - 8 + 4x = -3
5x = 5, x = 1
En remplaçant x par 1 dans E1 ou E2, on obtient: y = 2
Avant de passer aux questions, assurez-vous d'avoir en votre possession un crayon et du papier.
|| Équations à deux inconnues || Suite![]() ||
||